Ekonomi Mikro: Perilaku Konsumen

Teori Perilaku Konsumen

Barang-barang dan jasa merupakan seperangkat kebutuhan yang berguna untuk menjaga dan mempertahankan kelangsungan kehidupan manusia dari waktu ke waktu. Hal itu terjadi karena barang-barang dan jasa memberikan sesuatu yang sangat berharga, bagi pemakai atau disebut konsumen, yaitu berupa manfaat, kepuas an atau guna. Guna (utility) adalah “kepuasan“ yang diperoleh seseorang dalam mengkonsumsi suatu barang barang dalam waktu tertentu. Jika manfaat suatu barang meningkat maka berarti utilitas yang diperoleh dari mengkonsumsi barang tersebut menjadi lebih besar. Contoh, konsumsi barang kebutuhan pokok. Seseorang setelah mengkonsumsi barang-barang tersebut, dapat melihat dan merasakan sendiri manfaat serta utilitas yang diperolehnya, bahkan manfaat serta utilitas itu dirasakan selalu berubah dari waktu ke waktu. Fakta ini membuktikan orang-orang dapat hidup, tumbuh sehat serta berkembang sejalan dengan waktu, berkat mengkonsumsi berbagai jenis barang yang berguna

Tindakan orang dalam mengkonsumsi barang ternyata banyak dipelajari oleh ahli ekonomi dan membicarakannya dalam suatu konsep teori ekonomi yang disebut dengan teori perilaku konsumen. Sejak teori itu mulai dicetuskan hingga sekarang, terlihat teori perilaku konsumen terus mengalami perkembangan dari waktu ke waktu yakni:

1. Beberapa dari para ahli ekonomi Eropa tahun 1870-an yang dikelompokkan dalam Mashab Austria, mengemukakan teori tentang perilaku konsumen dan teori itu dikenal sebagai “teori nilai subjektif”. Tokoh-tokoh yang tekenal terkait dengan teori itu, adalah Karl Menger (Austria) Leon Walras (Prancis) dan W St Jevons (Inggris). Mereka itu mengembangkan teori nilai subjektif atas dasar pertimbangan berbagai faktor, seperti faktor-faktor psikologis, utilitas dan juga atas dasar pertimbangan tentang kesukaan dan kesulitan. Beberapa pelopor Mashab Austria beranggapan bahwa, nilai adalah hubungan antara manusia dan benda yang bersangkutan, dimana nilai suatu benda harus diterangkan berdasarkan fakta bahwa suatu benda mempunyai kapasitas untuk memenuhi suatu kebutuhan, dengan kata lain benda memiliki nilai sebab benda itu memberikan guna bagi subjek penilai.
2. Kemudian, teori nilai subjektif berkembang dengan nama “teori nilai modern”. Sebagai pencetus teori itu adalah Herman Heinrich Gossen, orang yang sangat terkenal karena hukum utilitas yang dikemukakannya. Dalam konsep teori peri laku konsumen ini, Gossen pertama-tama memperkenalkan konsep guna suatu barang, dan menuangkannya dalam hukum utilitas. Menurut Gossen bahwa tambahan kepuasan seseorang konsumen diperoleh dari tambahan mengkonsumsi suatu barang, dan tambahan utilitas yang diperoleh konsumen akan semakin berkurang jika ia mengkonsumsi barang itu secara terus menerus
3. Selanjutnya, pada abad ke-19, para ekonom seperti W Stanley Jevons, Leon Walras, dan Alfred Marshall, mengemukakan pemikirannya atas dasar anggapan berikut. Bahwa, utilitas itu dapat diukur seperti berat suatu barang. Mereka mencontohkan, beras dapat diukur dalam satuan kilogram, kwintal, ton, dan sebagainya. Dalam hal ini, konsumen dianggap dapat mengukur utilitas dengan suatu ukuran “cardinal”. Dengan kata lain, dianggap bahwa konsumen di dalam mengkonsumsi setiap barang atau kombinasi sejumlah barang dapat menunjukkan tingkat atau jumlah utilitas yang diperolehnya, dengan suatu ukuran kardinal atau angkaangka.
4. Dalam perkembangan lebih lanjut, anggapan-anggapan dari teori cardinal utility yang disebut di atas, masih dipandang sangat lemah serta terbatas. Dan keberatan prinsipiil terhadap ajaran nilai subjektif terletak pada masalah: ketidak-mungkinan untuk mengukur nilai atau guna dari suatu barang. Dikatakannya, bahwa seorang subjek ekonomi, hanya dapat merasakan dan kemudian membanding kan serta selanjutnya memaparkan dengan suatu pernyataan yang disebut preferensi. 

Dengan demikian, dasar teori nilai subjektif yang sudah ada ini diperhalus asas pemikirannya, yang kemudian memunculkan asas pemikiran baru mengenai skala-skala preferensi. Para ahli ekonomi kali ini mulai menampilkan asas pemi kirannya dengan konsep teori yang diilustrasikan melalui sebuah kurva yang disebut dengan “kurva indifferensi” Teori preferensi ini diajukan oleh Pareto, kemudian Hicks dan Allen sekitar tahun 1934. 

Pangkal tolak dari pemikiran para ekonom dalam wujud kurva indifferensi, didasarkan pada beberapa asumsi berikut

1) Seseorang atau konsumen dianggap mempunyai sejumlah pendapatan untuk dibelanjakan, guna membeli sejumlah barang dan jasa. 

2) Disamping itu, utilitas yang diperoleh konsumen dari mengkonsumsi barang-barang dan jasa, sesungguhnya tidak dapat diukur dengan angka-angka atau satuan berat lainnya, seperti ukuran dari beras, air, jalan dan lain-lainnya. 

3) Utilitas dalam mengkonsumsi suatu barang dan jasa sebenarnya hanya dapat diarahkan secara subjektif oleh orang yang mengkonsumsi barang dan jasa itu, dan hal ini dapat dinyatakan dengan suatu pernyataan dalam bentuk kata-kata bahwa ia merasa puas sekali, puas, tidak puas, dan sebagainya

Karena kepuasan itu tidak dapat diukur maka kemudian para ahli ekonomi mencoba untuk mencari jalan lain, yakni dengan cara membandingkan utilitas ini dengan satuan uang. Sehingga, di dalam pembicaraan konsep utilitas, yang dipersoalkan bukannya berapa banyak utilitas yang konsumen peroleh dalam mengkonsumsi suatu barang, tetapi yang lebih difokuskan tidak lebih daripada senilai berapa (contoh, dalam satuan rupiah) konsumen memperoleh kepuasan dari mengkonsumsi barang tersebut. 

Sebagai contoh ilustrasi, yakni seorang konsumen dengan pendapatan terbatas per bulan, berupaya untuk membelanjakan uang yang dimilikinya itu dengan lebih mengutamakan, antara lain kebutuhan pokok seperti beras yang harus dia sediakan untuk memenuhi kebutuhan sebulan, daripada kebutuhan-kebutuhan lain yang dianggap belum perlu untuk dibeli. 

Katakanlah, seorang konsumen ingin membeli kebutuhan pokok seperti komoditi beras di pasar. Dalam pembelian beras ini, kejadian yang biasa terjadi adalah tawar-menawar tentang harga beras per kilogram, antara konsumen dengan penjual. Konsumen mempertimbangkan untuk membeli katakanlah; 30 kilogram beras untuk dapat memenuhi konsumsi kebutuhan keluarga selama sebulan, dengan tingkat harga yang disepakati misalnya Rp 5.000 per kilogram. Maka, dengan kesepakatan harga setinggi itu, tentu konsumen sudah dianggap telah mempertimbangkan nilai utilitas yang ia peroleh dari pembelian beras sebanyak itu. Ini berarti bahwa, konsumen telah membandingkan uang yang ia bayar sebanyak Rp 5.000 kali jumlah beras yang dibeli sebanyak 30 kilogram. Kondisi seperti ini, dalam teori ekonomi biasa disebut dengan “keseimbangan konsumen” (consumers equilibrium).

Jika diperhatikan perilaku konsumen dalam pembelian beras ini, sesungguhnya ia tidak dapat mengukur utilitas yang diperoleh dari setiap kilogram beras yang dibeli, tetapi paling tidak ia telah menterjemahkan utilitas ini dengan sejumlah uang atau dengan sejumlah nilai uang yang ia telah keluarkan.

Dengan pokok pemikiran seperti tersebut di atas maka inti dari pembahasan teori pilihan konsumen, mengasumsikan bahwa:

1) Seorang konsumen dengan pendapatan tertentu, kemudian dihadapkan dengan sejumlah barang-barang dan jasa pilihan, maka tindakan yang ia lakukan adalah tidak akan membeli semua barang–barang dan jasa yang ia inginkan. Ia tentu harus melakukan pemilihan dan bahkan mepertimbangkan kembali, di antara bermacam-macam barang dan jasa yang ada itu dengan harga alternatif. 

2) Setiap konsumen mempunyai sebuah daftar preferensi (seperti suka, tidak sukan, atau yang lain perlu tidak perlu, dan lain-lain). Ia mengetahui, apakah sesuatu itu lebih baik atau lebih buruk, ataukah ia sendiri akan bersikap indifferensi (tidak memihak) terhadapnya. 

3) Konsumen ini memenuhi situasi yang terbaik di antara situa si yang dihadapi, dan situasi tersebut merupakan situasi keseimbangan. Ciri-ciri dari situasi yang sedemikian adalah bahwa pilihan di antara barang-barang dan jasa di luar itu sudah tidak mungkin diinginkan lagi.

Jadi dalam teori perilaku konsumen “dalil rasional“ merupakan hal yang umum sebagai pangkal tolak dari teori tersebut. Disini konsumen dianggap mempunyai pilihan atas berbagai alternatif yang tersedia untuknya, dalam berbagai bentuk yang dapat memenuhi kepuasannya, jika ia mengkonsumsi barang–barang dan jasa sebanyak-banyaknya. Ini membuktikan bahwa ia sadar atas berbagai alternatif yang dihadapinya dan ia pun dianggap mampu meng tasinya.

Dengan mengikuti perkembangan dari teori perilaku konsumen di atas, maka konsep utilitas dalam pembahasannya dibedakan menjadi dua bagian, yaitu: 

1) Utilitas kardinal (cardinal utility), yang menyatakan bahwa utilitas dapat diukur. 

2) Utilitas ordinal (ordinal utility), yang menyatakan bahwa utilitas tidak dapat diukur

Teori Utilitas 

Kardinal Berlandaskan beberapa pandangan dalam pemikiran teori perilaku konsumen, maka konsep pemikiran teori utilitas kardinal ini selanjutnya didasarkan atas beberapa asumsi. Asumsi yang dimaksud adalah:

• Bahwa nilai suatu barang itu tergantung pada penilaian subjektif dari konsumen.
• Bahwa utilitas ini dapat diukur. Dalam hal ini dianggap konsumen mempunyai ukuran kardinal atas tingkat atau jumlah utilitas dari mengkonsumsi barang tersebut. Contoh, utilitas dari mengkonsumsi sebuah mobil dinilai 50 util, mengkonsumsi sebuah sepeda motor dinilai 25 util dan lain-lain.
• Perbedaan jumlah utilitas suatu barang dapat diperbanding kan, dan perbandingan itu mengarah pada kenyataan sebagai berikut. Contoh, utilitas dalam mengkonsumsi sebuah mobil adalah 50 util, sebuah sepeda motor adalah 25 util, maka disini dapat dikatakan bahwa kepuasan konsumen di dalam mengkonsumsi sebuah mobil dikatakan dua kali lipat lebih tinggi, bila dibandingkan dengan mengkonsumsi sebuah sepeda motor.
• Tambahan utilitas dari mengkonsusi suatu barang akan semakin berkurang, bila konsumsi dilakukan secara terus menerus atau kontinyu, bahkan dapat mencapai tingkat maksimum dan seterusnya dapat mencapai nilai negatif.
• Konsumen bersikap rasional di dalam menentukan pilihan konsumsi terhadap suatu barang. Maksudnya, bahwa setiap konsumen dalam membelanjakan pendapatannya selalu mengarah kepada suatu pencapaian utilitas maksimum.
• Utilitas dapat diukur dalam satuan uang, maksudnya bahwa utilitas dapat dinilai dengan sejumlah uang sesuai dengan kesediaan membayar dari konsumen untuk mendapatkan satusatuan barang.
• Sebagai pengembangan asumsi dari e) di atas maka perlu kembali diasumsikan, bahwa utilitas marginal dari uang adalah konstan, dengan kata lain uang dianggap sebagai nilai subjektif yang konstan.
• Bahwa utilitas itu dapat ditambahkan, maksudnya bahwa utilitas total adalah merupakan penjumlahan utilitas dari; konsumsi barang pertama, barang kedua, dan seterusnya.
• Bahwa utilitas yang diperoleh dari mengkonsumsi suatu barang adalah bersifat bebas (independent). Ini dimaksud kan bahwa utilitas dari mengkonsumsi barang pertama itu tidak dipengaruhi oleh utilitas yang diperoleh dari mengkonsumsi barang kedua, dan demikian seterusnya. Namun demikian, asumsi yang terakhir ini diakui oleh banyak kalangan ahli masih tidak realistis. Contoh, orang yang memakai dasi akan memperoleh utilitas yang lebih tinggi, apabila pada saat yang sama, dia mengendarai sebuah mobil baru dibandingkan dengan mengendarai sebuah sepeda gayung. 

# Utilitas Total 

Herman Heirich Gossen mengemukakan hukum tentang utilitas total yang diperoleh seseorang dalam mengkonsumsi suatu barang dalam jumlah tertentu dan secara terus menerus. Hingga kini hukum itu dikenal dengan hukum Gossen pertama dan kedua. Hukum Gossen pertama pada intinya menyebutkan “bahwa sewaktu kita memenuhi kebutuhan suatu barang tertentu secara terus menerus, maka kepuasan yang dicapai akan semakin berkurang dan sampai akhirnya suatu saat akan mencapai utilitas yang maksimum, dan bila kebutuhan barang tersebut terus ditambah maka utilitasnya pun akan semakin menurun bahkan negatif”. Hukum Gossen pertama ini juga dinamakan dengan ”law of dimini shing utility”, yakni hukum kepuasan konsumen yang semakin berkurang. 

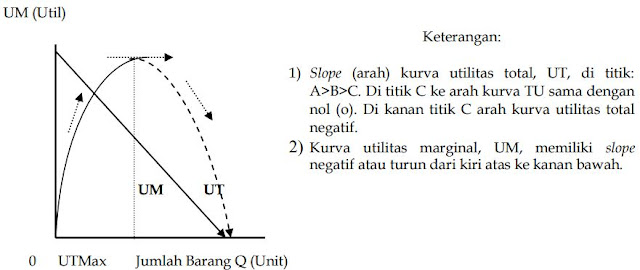
Hubungan kepuasan yang berkurang dengan jumlah barang yang dikonsumsi oleh konsumen, yang dapat dijelaskan dengan menggunakan sebuah kurva yang disebut kurva utilitas total. Hubungan utilitas total (UT) dengan jumlah barang yang dikonsumsi ditampilkan pada Gambar 65, dimana di sumbu vertikal dicantumkan variabel utilitas total dan di sumbu horizontal dicantumkan varaiabel jumlah barang tertentu atau sejumlah barang yang sama, yang dikonsumsi secara terus menerus

Dengan menggunakan pendekatan analisis matematika, selanjutnya hukum yang dikemukakan oleh Gossen ini dijelaskan. Pada konsumsi barang Q1 unit di titik A, utilitasnya dinilai 9 util. 

Pada konsumsi barang Q2 unit di titik B , utilitasnya dinilai 16 util. 

Pada konsumsi barang Q5 unit di titik C, utilitasnya dinilai 25 util. Pada konsumsi barang Q>5 unit setelah titik C, utilitas <25 util. Dan demikian seterusnya.

Gambar 65. Kurva Utilitas Total

Dengan memperhatikan data di atas maka terlihat utilitas mula-mula naik dari titik0 ke titik A dan terus ke titik B, hingga akhirnya sampai di titik maksimum C. Akan tetapi, kenaikan itu mengalami pertambahan yang menurun. Jika kebutuhan konsumsi terus dipenuhi maka utilitas terus mengalami pertambahan yang menurun bahkan negatif setelah melewati titik C maksimum. Ini menunjukkan bahwa “hukum utilitas total yang semakin berkurang“ (law of diminishing return) itu dinyatakan mulai berlaku setelah titik maksimum terlampaui.

Kemudian, dengan menggunakan pendekatan matematika hubungan kedua varaibel tersebut secara fungsional dinyatakan dengan persamaan: 

UT=f (Q) 

dimana: 

UT=utilitas total. 

Q=jumlah barang yang dikonsumsi.

Fungsi utilitas ini dapat dibaca demikian, yakni pada setiap titik (contoh A, B, C dan seterusnya) pada kurva utilitas total, merupakan koordinat dari pasangan nilai Q sebagai variabel bebas dengan nilai UT sebagai variabel terikat (dependent). Jika disusun pasangan dari variabel jumlah barang yang dikonsumsi dengan variabel utilitas total, hasilnya nampak seperti berikut:

Pada: Q    = 0……..1……..2…………….5 ……

Nilai: UT = 0……..9……..16…………..25……

Kurva utilitas total menunjukkan perkembangan yang degresif. Kenyataan ini dapat diperhatikan melalui Gambar 65. Kurva tersebut dipandang dari atas berbentuk cembung. Dengan bentuk kurva utilitas totak seperti ∩, menunjukkan suatu pertambahan konsumsi barang Q per unit yang menyebabkan utiliti total terus meningkat dengan pertambahan yang semakin menurun, bahkan dapat mencapai nilai nol (0) dan negatif. Lebih nyata, kondisi ini dapat dilihat melalui konsep teori utilitas marginalnya.

# Utilitas Marginal 

Ahli ekonomi pada abad ke-19 seperti Gossen beranggapan, bahwa tambahan utilitas yang diperoleh konsumen atas utilitas total atau disebut dengan kepuasan marginal (marginal utility), sebagai akibat dari pertambahan konsumsi per satuan barang akan menurun, jika ia terus memenuhi konsumsinya. Hubungan antara variabel pertambahan per satuan barang dengan variabel jumlah barang yang dikonsumsi, dinyatakan dengan sebuah kurva yang disebut kurva utilitas marginal (UM), seperti terpapar pada Gambar 66. Dalam Gambar 66, di sumbu vertikalnya dicantumkan variabel marginal utilitas, dan di sumbu horizontal tercantum variabel dari jumlah barang yang dikonsumsi. 

Gambar 66. Kurva Utilitas Marginal

Marginal utilitas dihitung dengan menggunakan rumus, sebagai berikut:

dimana; 

UM=utilitas marginal. 

∆UT= δ 

UT=pertambahan utilitas total. 

∆Q=δ 

Q=pertambahan jumlah barang yang dikonsumsi. 

# Hubungan Utilitas Marginal Dengan Utilitas Total 

Kurva utilitas total (UT) dan kurva utilitas marginal (UM) nampak memiliki hubungan yang erat, seperti diperlihatkan melalui Gambar 66.

1) UT mulai naik dari titik dimana Q=0, ke kanan atas sampai mendekati Q=5, dan pada saat ini UM pun masih bernilai positif, akan tetapi disini nilai UM-nya mengalami pertambahan yang semakin menurun. 

2) UT mencapai nilai maksimum di titik dengan Q=5, maka pada saat ini UM bernilai sama dengan nol (0). Atau UT masimum sama dengan UM nol (0). 

3) UT mulai mengalami penurunan pada saat “hukum kenaikan hasil yang semakin berkurang mulai berlaku”, yakni pada saat jumlah barang Q melewati titk dimana Q >5, dan pada saat ini pula nilai marginal utiliti atau UM-nya negatif dan bahkan UM pun terus menurun. 

Dengan memperhatikan kedua bentuk gambar di atas, yakni Gambar 65 dan Gambar 66, maka ternyata keduanya saling berhubungan seperti apa yang dijelaskan sebelumnya. 

# Fungsi Utilitas Total Dan Marginal Total 

Dengan menggunakan pendekatan fungsi matematika, hubungan yang saling mempengaruhi antara varaibel terikat (dependent) dengan variabel bebas (independent), dapat ditunjukkan sebagai berikut:

Pertama fungsi utilitas total:

UT=f (Q) 

dimana: 

UT=utilitas total sebagai varaibel terikat (dependent). 

Q=jumlah barang yang dikonsumsi sebagai variabel bebas (independent), 

f=notasi fungsi.  

Dengan menggunakan cara yang sama seperti utilitas total, maka dapat pula disusun fungsi utilitas marginal sebagai berikut:

Kedua fungsi utilitas marginal: 

UM=f (Q) 

UM=∆ UT/ ∆Q 

Atau: UM=δ UT / δ Q

Selanjutnya, hubungan fungsional utilitas total dan utilitas marginal seperti tersebut di atas, dapat dijelaskan dengan menggunakan contoh data pada Tabel 14. Misalkan saja, seorang konsumen mengkonsumsi buah mangga secara berturut-turut sebanyak 6 buah. Konsumen beranggapan, bahwa utilitas yang ia peroleh dari mengkonsumsi buah mangga ini dapat diukur dengan angka atau satuan util. Dan data jumlah mangga yang dikonsumsi serta utiliti total yang diperoleh konsu men dicantumkan pada Tabel 14. Kemudian data utilitas pada Tabel 14 itu dapat dibaca, yaitu utilitas yang diperoleh konsumen dari mengkonsumsi buah mangga adalah sebagai berikut:

Mangga ke I, memberikan utilitas yang dinilai =9 util. 

Jadi nilai utiliti total (UT) =9 util. 

Mangga ke II, memberikan utiliti yang dinilai =7 util. 

Jadi nilai utiliti total (UT), adalah 9 util+7 util=16 util. 

Mangga ke III, memberikan utilitas yang dinilai =5 util.

Jadi nilai utilitas total (UT) adalah 16 util+5 util=21 util. 

Demikian seterusnya untuk konsumsi mangga yang lainnya. Seperti diperlihatkan dalam Tabel 14.

Pola utilitas total seperti data dalam Tabel 14 memperlihatkan terjadinya peningkatan dari 0 hingga 25, namun setelah men capai puncak/maksimum nilainya nampak kembali menurun. Dan disini diketahui pula pola peningkatan nilai UT ini dengan pertambahan yang menurun dari setiap tambahan satu unit mangga yang dikonsumsi konsumen. 

Tabel 14. Data Analisis Utilitas Total Dan Utilitas Marginal

Keterangan:

1) Utilitas marginal *UM dihitung dengan rumus: UM=∆ UT/∆Q (util), dimana ∆=nilai perubahan. 

2) Utilitas marginal **UM dihitung dengan rumus: UM=δ UT/δ Q (util), dimana δ=nilai perubahan sekecil- kecilnya (differensial). 

Demikian pula pola nilai dari utilitas marginal terlihat dengan arah nilai yang terus menurun dengan terja dinya tambahan satu unit tambahan konsumsi mangga dari konsumen. Ini menandakan bahwa pola dari nilai UM adalah terus menurun sampai titik nol bahkan dapat bernilai negatif.

Gambar 67. Fungsi TU dan MU

Bila data utilitas total dan utilitas marginal dalam Tabel 15 dinyatakan dalam bentuk fungsi maka hasil analisisnya , adalah sebagai berikut:

1) Fungsi UT…………Dengan bentuk fungsi parabola

2) Fungsi UM……….. Dengan bentuk fungsi garis lurus

# Tingkat Substitusi Marginal Barang (X – Y) 

Hukum Gossen kedua, pokok bahasannya adalah dengan bermacam-macam kebutuhan yang ada, maka setiap orang akan membagi alat-alat, atau dapat juga dikatakan pendapatan yang dimilikinya, sedemikian rupa untuk bermacam-macam kebutuhan, sehingga masing-masing kebutuhan itu terpenuhi dengan tingkat kepuasan yang sama. Dengan kata lain, dalam hal memuaskan kebutuhan maka setiap orang akan berusaha mencapai suatu keadaan dimana pemenuhan kebutuhannya seimbang.

Untuk menjelaskan hukum Gossen ini, seorang ahli ekonomi Karl Menger, telah menyusun skema kebutuhan dengan tetap mempersoalkan, bagaimana seorang konsumen akan membagi pendapatan mereka untuk bermacam-macam barang dan jasa yang dibutuhkan, bilamana harga barang dan jasa itu sudah diketahui sebelumnya. Untuk maksud tersebut, disusun sebuah skema tentang jenis barang dan jasa yang dibutuhkan seorang konsumen. Contoh, untuk kebutuhan sandang, pangan, perumahan, dan lain-lain. 

Dengan memperhatikan data yang tercantum dalam Tabel 15, maka diketahui bagaimana alokasi pendapatan konsumen untuk berbagai macam kebutuhan. Disini dinyatakan bahwa konsumen dalam mengalokasikan sejumlah pendapatannya yang terbatas, dianggap akan lebih mengutamakan untuk memenuhi kebutuhan pangan. Dia menilai tingkat utilitas total yang diperoleh, adalah sebesar 6 util. Dengan keterbatasan pendapatan ini berarti konsumen tidak dapat memenuhi kebutuhan lain selain pangan

Menurut hukum Gossen kedua, kondisi itu dikatakan belum mencapai seimbang dengan kata lain utilitas belum maksimum. Sebab, masih ada kebutuhan yang tidak terpenuhi selain pangan.

Tabel 15. Skema Kebutuhan Barang Konsumsi Seorang Konsumen

Agar lebih seimbang, kiranya konsumen akan berusaha untuk menambah jenis barang yang akan dikonsumsi. Misalnya, sekarang pilihan pada barang kedua, yaitu sandang. Dengan mengkonsumsi dua jenis barang ini, konsumen menilai utilitas yang diperoleh untuk kedua jenis barang dengan nilai yang sama yaitu pangan sama dengan 5 util dan sandang juga 5 util, sehingga utilitas total meningkat dari hanya 6 util menjadi 10 util. Dan perlakuan sedemikian terus dilakukan, untuk jenis kebutuhan konsumsi yang lain, seperti perumahan, pendidikan, dan lain-lain. Dengan semakin bertambahnya kebutuhan konsumsi konsumen, maka akan terjadi peningkatan utilitas hingga ke tingkatan yang maksimum, yakni pada saat utilitas total mencapai 12 util. 

Dengan menggunakan data pada Tabel 15 di atas ternyata utilitas total bernilai 12 util ada sebanyak dua angka. Oleh karena itulah, disini disarankan “dalam menentukan nilai utilitas maksimum”, yang paling tepat adalah menggunakan syarat pada saat mana utilitas marginal: UM=0. Atau dengan menentukan terlebih dahulu syarat keseimbangan konsumen, dimana perbandingan dari utilitas marginal terhadap harga per unit dari setiap jenis barang adalah sama bagi seluruh barang. 

Dua konsep tentang utilitas marginal (UM) dengan tingkat substitusi marginal ini, dipakai sebagai dasar penentuan keseimbangan konsumen dalam mengkonsumsi dua jenis barang atau lebih. Pertama diasumsikan, bahwa konsumen hanya mengkonsumsi dua jenis barang saja, yaitu barang X dan barang Y.

1) Katakanlah, pada suatu saat konsumen ingin mengurangi jumlah konsumsi barang X sebesar 1 unit. Dengan konsumsi barang X yang menurun 1 unit tentu saja akan mempengaruhi utilitas marginal barang X. Hal ini dapat dijelaskan dengan cara berikut; konsumsi barang X turun 1 unit dinyatakan dengan ∆ X=1 unit. 

Penurunan konsumsi barang X ini mempengaruhi utilitas marginalnya, yaitu sebesar, U

UMx=∆ UT/∆X. 

Karena nilai dari ∆ X = 1 unit, maka: 

UMx=∆ UT/∆X 

UMx=∆UT/1

Atau UMx=∆ UT………….……….(a).

Dengan penurunan konsumsi barang X=1 unit, dan juga dengan asumsi bahwa pendapatan konsumen adalah konstan, maka konsumen pun cenderung mensubstitusi barang X dengan barang Y, mengingat pendapatan konsumen sekarang dialihkan ke barang Y.

2) Andaikata sekarang konsumen menambah konsumsi barang Y sebesar ∆Y sebagai pengganti dari berkurangnya konsumsi barang X, maka pertambahan konsumsi barang Y ini akan menyebabkan utilitas marginal barang Y berubah menjadi:

3) Selanjutnya, persamaan (1) dengan persamaan (2) di atas digabung, maka akan menghasilkan persamaan baru, yaitu: 

4) 

dimana TSMx = tingkat substitusi marginal barang X-Y (Marginal Rate of Substitution X-Y). Jadi tingkat substitusi konsumsi barang X terhadap barang Y menunjukkan bahwa setiap mengganti barang X sebesar 1 unit yang tidak lagi dikonsumsi, maka konsumen ini tidak cukup hanya menggantikannya dengan barang Y sebesar ∆Y, tetapi juga harus ∆Y ini dikalikan lagi dengan UMy-nya, dengan asumsi bahwa pendapatan konsumen adalah konstan.

# Utilitas Marginal Dan Pendapatan 

Diketahui bahwa harga barang X dan harga barang Y tertentu dan juga pendapatan juga tertentu besarnya. Misalkan, pendapatan konsumen meningkat sebesar Rp 1. Seberapa besar utilitas tambahan konsumen ini akan naik? Jawaban atas kejadian ini adalah sebagai berikut: 

1) Andaikata tambahan pendapatan (I) sebesar Rp 1 ini, digunakan untuk membeli barang X saja, maka jumlah barang X yang akan diperoleh, adalah sebanyak:

I=Px.X 

1=Px.X 

Atau: X=1/Px unit. 

Dengan kata lain, jumlah konsumsi barang X sebanyak 1/Px unit. Dengan kenaikan jumlah barang X sebesar 1/Px unit ini tentu mempengaruhi utilitas marginal konsumen. 

Bila ∆ X=1/Px unit, maka utilitas total konsumen akan naik yaitu:

Jadi tambahan pendapatan sebesar Rp 1 akan menyebabkan utiliti total konsumen (∆UT) akan naik sebesar UMx .Px.

1) Hal yang sama berlaku juga bila kenaikan pendapatan sebesar Rp 1 ini hanya digunakan untuk membeli barang Y saja. Akibatnya utiliti total (∆UT) konsumen untuk barang Y ini naik, yaitu sebesar Umy. Py. 

2) Hasil perhitungan pada bagian 1) dan 2) di atas masing-masing menunjukkan; 

∆UT=UMx. Px. 

dan ∆UT=UMy. Py. 

Hasil yang tersebut terakhir ini sama artinya dengan utilitas marginal per rupiah dari pengeluaran setiap barang yang dibeli oleh konsumen. 

# Keseimbangan Konsumen 

Agar konsumen mendapatkan posisi yang optimum atau dikatakan konsumen mencapai keseimbangan, maka secara rasional ia akan berusaha mencapai utilitas yang maksimum di dalam mengkonsumsi suatu barang dalam jangka waktu tertentu. Untuk menjelaskan keberadaan dari posisi keseimbangan ini, berikut ditunjukkan cara menganalisisnya satu persatu dengan asumsi jumlah barang yang dikonsumsi:  

* Keseimbangan konsumen dengan konsumsi barang X. 

* Keseimbangan konsumen dengan konsumsi barang X – Y

(1) Keseimbangan Konsumen – Barang X 

Kondisi keseimbangan konsumen dalam mengkonsumsi satu jenis barang, misalnya barang X, dapat ditunjukkan melalui kesamaan berikut: 

UMx = Px

Hasil kesamaan ini menunjukkan agar konsumen mencapai keseimbangan. Maka diperlukan suatu kesamaan dari harga barang X dengan utilitas marginal dari barang X. Artinya bahwa konsumen membayar barang X seharga Px sesuai dengan perolehan tambahan utilitas per unit barang X.

Dengan menggunakan analisis matematika posisi konsumen dalam mencapai kepuasan maksimum diperlukan syarat maksimumkan utiliti total, dengan kata lain: selisih (diskriminasi) D antara utiliti total dengan pengeluaran total untuk barang X adalah sebesar-besarnya. 

Analisis diskriminan D dilakukan dengan cara berikut: 

a) Susun fungsi UT. Agar fungsi D-nya mencapai maksimum, maka diperlukan suatu syarat, yaitu differensial pertama dari fungsi D yang disamakan dengan nol (0). Atau dinyatakan dengan D΄ = 0.

b) Kemudian dihitung differensial dari fungsi D, yaitu:

(2) Keseimbangan Konsumen – Barang X Dan Y

Untuk memenuhi konsumsi dua jenis barang yakni X dan Y maka ia harus mengalokasikan pendapatannya di antara kedua jenis barang tersebut. Pendapatan konsumen sebesar I dialokasikan untuk barang X dan Y, sedemikian rupa sehingga dicapailah suatu tingkatan utiliti total yang memiliki kemungkinan tertinggi. Untuk maksud tersebut, kiranya perlu ditentukan kondisi optimum yang harus dipenuhi untuk mencapai utiliti total yang maksimum. 

Dengan pertimbangan bahwa utilitas marginal dari Rp 1 pengeluaran untuk barang X adalah UMx/Px (lihat pembahasan di atas). Dan tentu hal itu, semestinya sama juga berlaku bagi barang Y, yaitu UMy/Py. Disini kita berargumentasi bahwa kondisi optimum konsumen tercapai, semestinya pada saat jumlah kedua jenis barang tersebut adalah sama

Agar dapat melihat kondisi tersebut di atas benar-benar terjadi, maka disini perlu dianalisis satu persatu, yaitu dengan cara:

Pertama:

a) Kondisi dimana:…………….UMx/Px > UMy/Py 

Dengan memperhatikan kondisi tersebut, maka bagi konsu men ada cara-cara yang dapat dilakukan, agar utiliti yang diperoleh meningkat. Untuk itu, konsumen paling tidak mengurangi pengeluaran untuk kebutuhan barang Y sebanyak Rp 1 dan kemudian digunakan untuk membeli barang X yang lebih banyak. Dengan cara tersebut berarti bahwa ada suatu pengorba nan dari utilitas sebesar UMy/Py unit. Dan perlakuan yang sedemikian itu perlu dicoba dengan cara berulang-ulang sehingga pada akhirnya akan dicapai kondisi yang lebih baik yakni membawa jumlah UMx/Px=UMy/Py.

b) Kondisi dimana:……………UMx/Px < UMy/Py 

Bila sekarang yang terjadi adalah kondisi kebalikannya, ini berarti konsumen perlu melakukan pengurangan pengeluaran untuk kebutuhan barang X sebesar Rp 1 dan digunakan untuk membeli barang Y yang lebih banyak. Dengan melakukan itu, berarti ada pengorbanan utiliti sebesar UMx/Px unit dari barang tersebut. Dal perlakuan yang sedemikian itu, kembali dicoba dilakukan berulang-ulang. Sehingga pada akhirnya akan dicapai kondisi yang lebih baik, yakni membawa jumlah UMx/Px=UMy/Py, menjadi sama. 

c) Kondisi dimana…………….UMx/Px < UMy/Py 

Andaikata kondisi yang ada adalah pada posisi keseimbangan, yaitu kesamaan antara UMx/Px=UMy/Py, maka ini menun jukkan bahwa kondisi optimum konsumen telah tercapai. Posisi seperti ini menandakan terjadinya keseimbangan konsumen. Jadi syarat keseimbangan yang harus terpenuhi, adalah UMx/Hx=UMy/Hy. Kondisi yang sama seperti ini berlaku sama untuk lebih dari dua jenis barang, yakni x,y,z………….n. 

(3) Keseimbangan Konsumen – Dengan Anggaran 

Dengan anggaran sebesar I yang jumlahnya tertentu konsumen mengkonsumsi dua jenis barang yaitu X dan Y, dan tingkat harga masing-masing adalah Px dan Py. Secara rasional konsumen berusaha untuk mendapatkan kepuasan total dari mengkonsumsi kedua jenis barang tersebut dengan mengalokasikan pendapatannya yang terbatas sebesar Rp I, agar tetap mencapai kepuasan maksimal. Untuk maksud tersebut, maka konsumen harus berusaha untuk menentukan perbedaan yang terbesar (diskriminan) D antara utiliti total dari mengkonsumsi barang X dan Y: 

I=Px. X + Py.Hy 

Dengan analisis matematika perhitungannya dilakukan adalah: 

a). Susun fungsi diskriminan D: 

D=[ UTx + UTy] – [ Px.X + Py.Y] 

dimana D = fungsi UT yaitu [UTx + UTy].

b). Fungsi di atas dihitung differensial parsial: 

δ D=δ [ UTx + UTy] – δ [ Px.X + Py.Y] 

c). Differensial parsial I terhadap X: 

δ D/δX=δ UTx/ δX – Px δX/ δX 

Agar mencapai maksimum maka syaratnya adalah: 

δ D/δX= 0 

δ UTx/δX – Px δX/ δX = 0 

δ UTx/δX= Px 

UMx=Px………………………….(1) 

d). Differensial parsial I terhadap Y: 

δ D/δY=δ UTy/ δY – Py δY/ δY 

Agar mencapai maksimum maka syaratnya adalah: 

δ D/δY=0 

δ UTy/δY – Py δY/δY=0 

δ UTy/δY =Py 

UMy=Py……………………..….(2)

e). Berdasarkan hasil perhitungan differensial parsial di atas, selanjutnya dapat ditentukan keseimbangan konsumen untuk: 

*Barang X……syaratnya: UMx=Px. 

*Barang Y……syaratnya: UMy=Py. 

*Dan kombinasi dari keseimbangan barang X dan Y, maka dapat ditentukan keseimbangan konsumen untuk barang X dan Y, yaitu:

Dengan demikian keseimbangan konsumen dalam mengkonsumsi dua jenis barang tercapai pada saat adanya kesamaan antara perbandingan utilitas marginal masing-masing barang dengan harga masing-masing barang tersebut. 

Atau:

Surplus Konsumen – Kurva Permintaan 

Umumnya dapat dikatakan, bahwa semakin banyak suatu barang dikonsumsi maka tambahan utilitas yang diperoleh akan semakin mengecil. Bahkan, jika sangat banyak barang itu dikonsumsi dapat membosankan atau dikatakan tidak lagi memberikan utilitas. Dengan demikian, dapat diartikan pula bahwa konsumsi barang ke pertama akan memberikan utilitas tertinggi, dibandingkan dengan barang yang kedua, ke tiga dan seterusnya, jika kegiat an konsumsi itu dilakukan secara terusmenerus.Jika dikembalikan pembicaraan ini ke persoalan konsumsi buah mangga sebelumnya, dengan menggunakan data Tabel 16, maka utilitas yang semakin menurun ini ditampilkan melalui nilai dari utilitas maginalnya.

Oleh karena, satuan tambahan utilitas ini dimanipulasi dalam satuan uang (Rp) yang dipakai sebagai petunjuk kesediaan konsu men membayar, maka kali ini dinyatakan bahwa untuk konsumsi mangga ke pertama konsumen akan menerima utilitas marginal sebesar 8 util (lihat Tabel 16). Dan hal ini berarti pula bahwa konsumen berani menilai utilitas marginal itu dengan satuan uang. Sebesar Rp 8.000/util. Kemudian untuk mangga kedua, karena utilitas marginal yang diperoleh konsumen lebih kecil, yakni hanya dinilai 6 util, maka konsumen cuma berani menilai utilitas marginal tersebut dengan satuan uag Rp 6.000/util. Demikian seterusnya, untuk utilitas marginal dari mangga ketiga, keempat dan yang lain nya, karena dinilai semakin mengecil maka utilitas marginalnya pun dinilai semakin rendah dalam satuan uang, seperti disajikan dalam Tabel 16.

Tabel 16. Jumlah Mangga, Nilai Marginal Dan Surplus Konsumen

Dengan dasar penilaian seperti disebutkan di atas, kemudian dapat disusun data tentang penilaian konsumen terhadap utilitas marginal dari setiap unit mangga yang dikonsumsi oleh konsumen. Dan ternyata hubungan antar data nilai utilitas marginal dari setiap unit mangga yang dikonsumsi menampakkan arah yang semakin menu run, jika jumlah mangga yang dikonsumsi itu semakin bertambah banyak. Lihat data pada Tabel 16.

# Surplus Konsumen 

Jika sekarang diumpamakan bahwa harga pasar untuk sebuah mangga adalah Rp 4.000/buah. Kemudian, dicoba untuk dihitung besar surplus yang diperoleh konsumen dari kegiatan mengkonsumsi buah mangga, pada berbagai tingkatan harga yang mana sesungguhnya konsumen bersedia untuk membayar.

Surplus konsumen adalah selisih antara harga pasar suatu barang dengan kesediaan konsumen membayar suatu barang, yang disesuaikan dengan utilitas marginal yang ia terima pada saat mengkonsumsinya. Karena harga pasar mangga adalah Rp 4.000/buah, sedangkan untuk mangga ke pertama konsumen sesungguhnya bersedia membayar Rp 8000 dan disini dikatakan bahwa konsumen memperoleh surplus sebesar Rp 8.000– Rp 4.000=Rp 4.000.

Untuk mangga kedua, dimana konsumen sesungguhnya bersedia membayar mangga dengan Rp 6.000/buah, tetapi karena harga pasar mangga hanya Rp 4000/buah, maka disini dikatakan konsumen memperoleh surplus sebesar Rp 6.000 – Rp. 4.000=Rp. 2.000, demikian seterusnya, data surplus konsumen dapat dihitung lebih lanjut. Dan, data surplus konsumen ini telah dicantumkan pada Tabel 16.

Untuk melihat lebih lanjut tentang hubungan antara variabel jumlah barang yang dikonsumsi dengan besarnya surplus konsumen dari mengkonsumsi mangga ini, dapat dilihat pada Gambar 16. Surplus konsumen dihitung sebagai berikut:

Pada tingkat harga Rp. 4.000 jumlah mangga=3 buah. 

Pada tingkat harga Rp. 10.000 jumlah mangga =0 buah

Rumus:

Jadi surplus konsumen dapat ditunjukkan melalui bidang yang dibatasi oleh kurva nilai marginal dengan tingkat harga dan jumlah barang di tingkat pasar. (Lihat Gambar 68). 

Andaikata kurva permintaan barang disini tidak berbentuk sebuah garis lurus, maka perhitungan surplus konsumen dilakukan dengan menhitung luas bidang yang dibatasi kurva permintaan yaitu dibawah kurva permintaan bukan garis lurus, dengan garis harga dan jumlah barang di tingkat pasar. Rumus menghitung surplus konsumen disini menggunakan perhitungan integral seperti yang dijelaskan pada bagian analisis konsumer surplus dan produser surplus

Gambar 68. Kurva Nilai Marginal Dan Surplus Konsumen

# Kurva Permintaan Dan Nilai Marginal 

Konsumen dalam menilai utilitas marginal dari konsumsi barang per unit menggunakan satuan uang (misalnya Rupiah) sebagai cara untuk memanipulasi satuan util, dan ini menunjukkan tanda kesediaan membayar atas utilitas yang diperolehnya. Oleh karena, dalam pembahasan di atas telah disebutkan bahwa nilai utiliti marginal per unit mangga ini diukur dengan Rp/util, sehingga satuan utilitas marginal ini berarti sama dengan Rp/ buah. 

Sekarang dapat dijelaskan kembali bahwa nilai marginal ini sama dengan harga per unit barang, karena itu pula kurva nilai utilitas marginal (UM) ini sekaligus dipakai menunjukkan kurva permintaan suatu barang dari seorang konsumen. Adapun bentuk kurva nilai utilitas marginal dan kurva permintaan mangga disini sebagai contoh, adalah turun dari kiri atas ke kanan bawah, sesuai dengan hukum permintaan barang Gambar 69 dan Gambar 70.

Dengan memperhatikan satuan utilitas marginal yaitu satuan Rp/util dan kurva permintaan diukur dengan satuan Rp/unit, ini berarti bahwa satuan per util itu dimanipulasikan dengan satuan Rp/unit, dan kedua satuan tersebut selanjutnya Gambar 68. Kurva Nilai Marginal Dan Surplus Konsumen Harga (Rp.000/Buah) 10 4 NM 0 1 3 Jumlah Barang (Buah/hari) Keterangan: * Luas bidang segitiga yang diarsir hitam menunjukkan SK=surplus konsumen. * NM=kurva nilai marginal. SK dinyatakan sama. Oleh karena itu, kurva nilai utilitas marginal adalah sama dengan kurva permintaan. Lihat data pada Tabel 16 pada kolom 2 dan 4.

Keterangan: 

1. Satuan pada kurva nilai utilitas marginal (NM) yakni Rp/util 

2. Satuan pada kurva permintaan barang (d) yakni Rp/buah. 

3. Nampak disini satuan Rp/util di kurva nilai utilitas marginal ini dimanipulasi dengan Rp/buah pada kurva permintaan barang. 

Teori Utilitas Ordinal 

Dalam pandangan ahli ekonomi yang tidak setuju dengan pandangan nilai subjektif beranggapan, bahwa dalam teori utilitas kardinal, asumsi yang dikemukakan adalah sangat terbatas. Oleh karena itu, mereka kemudian mengadakan modifikasi terhadap asumsi tersebut, dalam teori utilitas ordinal. Adapun asumsi yang dikemukakan dalam teori utilitas ordinal, adalah: 

1. Utilitas ini tidak dapat diukur, sebagaimana halnya menggunakan angka dalam satuan.
2. Utilitas yang diperoleh seorang konsumen dari mengkonsumsi suatu barang hanya dapat dinyatakan dengan preferensi, yakni dalam bentuk suatu pernyataan seperti; suka, lebih suka, sangat suka, dan lai-lain. Dalam menentukan preferensi, setiap perilaku individu dalam konsumsi 

didasarkan atas, dalil-dalil rasionalitas yang dinya takan sebagai berikut.

1. Untuk semua pasang kemungkinan dari pilihan A dan B, konsumen mengetahui, apakah ia lebih suka A daripada B atau lebih suka B daripada A, atau apakah ia bersikap sama (tidak memihak A atau B). 
2. Hanya ada satu dari tiga kemungkinan yang benar untuk berbagai pasang pilihan.
3. Jika konsumen lebih menyukai A daripada B, B daripada C, maka konsumen akan lebih menyukai A daripada C. Pernyataan yang terakhir ini menyatakan bahwa konsumen adalah konsisten atau transitif. Contoh, jika ia lebih suka mobil mercy daripada sepeda motor, dan lebih menyukai sepeda motor daripada sepeda gayung, maka dengan konsisten mengatakan bahwa ia lebih menyukai mobil mercy daripada sepeda gayung. 

Dengan dasar pemikiran seperti diuraikan di atas, maka dianggap konsumen mengetahui skala-skala preferensinya dank arena itu perilaku konsumen dapat digambar dengan sebuah kurva indifferensi. Kurva indifferensi menunjukkan berbagai kombinasi dari jumlah barang yang dikonsumsi oleh konsumen, yang dinilai memberikan utiliti/kepuasan sama. Kurva indifferensi ini kemudian digunakan sebagai dasar untuk menurunkan kurva permintaan suatu barang.

# Kurva Indifferensi 

Bila ingin mengulas lebih jauh sebuah kurva indifferensi, maka sedari awal yang perlu diketahui, adalah bahwa konsumen diasumsikan memiliki sejumlah pendapatan yang siap dibelanjakan (disposable income), untuk membeli sejumlah barang dan jasa guna memenuhi kebutuhannya. Guna memudahkan analisis maka disini dianggap bahwa konsumen dapat menilai, apakah ia: 

1) Lebih banyak menginginkan barang X ataukah barang Y atau sebaliknya. 

2) Ataukah, konsumen hanya menginginkan barang X saja, atau hanya menginginkan barang Y saja. 

3) Ataukah, konsumen bersikap indifferen terhadap kombinasi bagaimana pun juga dari barang X dan barang Y.

Dengan perasaan seseorang dapat mengetahui bahwa pilihan konsumen sangat kompleks batasannya, jika ia memiliki urutan dari sejumlah barang sesuai dengan keinginannya. Seseorang dapat membuat gambaran bahwa ketika konsumen memiliki pendapatan ia dapat menyusun daftar, atas barang yang dapat ia beli dengan satu rupiah, dalam urutan yang menurun dari apa yang paling disukai. Dalam hal ini, konsumen memulai dari urutan teratas yang menunjukkan paling disukai, kemudian menyusul yang lain yang semakin kurang disukai, hingga pendapatan mereka mencukupi. Konsumen tidak perlu mengganggap bahwa ia memiliki ukuran kardinal untuk suatu utilitas. 

Sebagai ilustrasi, pada Gambar 71. dikemukakan kombinasi dari barang X dengan barang Y dapat diperlihatkan sebagai berikut: 

Pada jumlah barang X=1,   jumlah barang Y=12. 

Pada jumlah barang X=2,   jumlah barang Y=6.

Dan demikian seterusnya untuk kombinasi barang X dengan barang Y yang lain, dapat ditentukan lebih lanjut. Semua kombinasi yang berbeda-beda dari barang X dan Y tersebut, ternyata memberikan tingkat kepuasan yang sama karena terletak pada satu kurva utilitas U yang bernilai 10 (atau U=10). Untuk jelasnya dapat dilihat melalui Gambar 71.

Gambar 71. Kurva Indifferensi

Sebuah kurva indifferensi adalah sebuah garis yang menun jukkan kombinasi dua barang yang oleh konsumen dinilai memberikan utilitas sama. Untuk menggambarkan sebuah kurva indifferensi, pada sumbu vertikal dicantumkan variabel jumlah barang Y (unit) yang dikonsumsi, dan pada sumbu horizontal dicantumkan barang X (unit) yang dikonsumsi. Kombinasi barang X dan barang Y yang terletak di satu kurva indifferensi, dikatakan bahwa kombinasi yang berbedabeda tersebut memberikan utilitas sama. Sebagai contoh, kombinasi di titik A dan di titik B pada Gambar 71.

Asumsinya, bahwa setiap orang mengetahui persis berapa penghasilan mereka sehari / seminggu / sebulan / setahun dan sebagainya. Dalam waktu tertentu itu, ia harus membelanjakan penghasilannya yang tertentu untuk membeli barang-barang dan jasa yang dibutuhkan. Bila hanya ada dua jenis barang yang dibeli atau dikonsumsi (contoh, barang X dan barang Y) dalam waktu tertentu, maka tempat kedudukan dari titik koordinat barang X dan barang Y (misalkan di titik A dan di titik B), adalah menunjukkan kombinasi dari konsumsi kedua jenis barang tersebut dan garis ini dinamakan sebuah kurva indifferensi. Jadi, sebuah kurva indifferensi menunjukkan tempat kedudukan dari titik-titik kombinasi dari jumlah barang X dan barang Y yang dikonsumsi oleh seorang konsumen, dan memberikan tingkat kepuasan sama.

# Fungsi Utilitas 

Sebuah kurva indifferensi dapat ditunjukkan dengan sebuah persamaan yang disebut dengan fungsi utilitas. Bentuk umum fungsi utilitas dinyatakan sebagai berikut:

U=f (X;Y) 

dimana: 

U=nilai utilitas (util). 

X=jumlah barang X (unit) yang dikonsumsi. 

Y=jumlah barang Y (unit) yang dikonsumsi. 

Contoh Ilustrasi – Pendekatan Matematika 

Fungsi utilitas seorang kosumen dinyatakan dengan: 

U=XY 

Dengan mengetahui fungsi utilitas seorang konsumen, maka kombinasi dari jumlah barang yang dikonsumsi yakni barang X dan barang Y, dapat ditentukan posisinya pada sebuah kurva indifferensi dan hasil kombinasi itu juga menunjukkan tingkat utilitas yang dicapai konsumen. Kejadian seperti itu, dapat dicoba dengan menggunakan berbagai pasangan barang X dan Y, seperti berikut.

Pada jumlah X=1 unit, maka jumlah barang Y=10 unit. 

Pada jumlah X=2 unit, maka jumlah Y=5 unit. 

Pada jumlah X=5 unit, maka jumlah Y=2 unit. 

Dan pada kombinasi barang X dan barang Y seperti tersebut di atas, hasil utilitas yang diperoleh konsumen adalah sebesar U=10 util. Dan dengan demikian maka dikatakan, bahwa konsumen memiliki satu buah kurva indifferensi. 

Dalam bentuk fungsi utilitas kurva indifferensi konsumen tersebut, dapat disusun dengan sebuah persamaan berikut sebagai contoh, dengan bentuk fungsi hiperbola.

U=Q1Q2+Q2+6Q1+6

Untuk menentukan jumlah barang Q1 dan Q2 yang dikonsumsi konsumen mencapai tingkatan maksimum pada nilai utilitas U=30, maka pemecahannya sebagai berikut

U=1Q2 + Q2 + 6Q1 + 6 

30=Q1Q2 + Q2 + 6Q1 + 6 

30=(Q1 + 1) (Q2 + 6) 

Dengan: 

Asimtot horizontal Q1=-1 

Asimtot vertikal Q2=-6.

Pada Gambar 72 diperlihatkan, garis asimtot Q1=-1 yang posisinya vertikal dan asimtot Q2=-6 posisinya horizontal. Dengan menggunakan persamaan hiperbola diatas dapat ditentukan Nilai maksimum untuk Q1 dan Q2 sebagai berikut: 

Gambar 72. Kurva Indifferensi (Id)

Bila dinyatakan Q1= 0 maka nilai ini disubstitusi ke persamaan berikut: 

30=(Q1 + 1) (Q2 + 6) 

30=(0 + 1) (Q2 + 6) 

30=(Q2 + 6) 

Q2=30 -6 

Q2=24 uni. 

Bila dinyatakan Q2= 0 maka nilai ini disubstitusi ke persamaan berikut: 

30=(Q1 + 1) (Q2 + 6) 

30=(Q1 + 1) (0 + 6) 

30=(6Q1 + 6) 

Q1=(30 -6)/6 

Q1=4 unit 

# Peta Indifferensi 

Nilai parameter utilitas (U) sudah barang tentu dapat berubah-ubah yakni naik atau turun. Perubahan nilai U ini nantinya ditunjukkan melalui pergeseran kurva indifferensi, misalnya pergeserannya naik berarti nilai U-nya bertambah besar dan sebaliknya jika kurva indifferensi bergeser turun maka berarti nilai U-nya bertambah kecil dari nilai mula-mula. (lihat pada Gambar 73).

Dengan kurva indifferensi Id2 berada di sebelah kanan dari kurva indifferensi Id1, maka dari sini diketahui bahwa semakin ke kanan posisi kurva indifferensi berarti semakin tinggi utilitas yang diperoleh oleh seorang konsumen dalam mengkonsumsi barang tersebut. Dan kumpulan kurva indifferensi dengan nilai utilitas yang berbedabeda, disebut dengan peta indifferensi. 

Gambar 73. Peta Kurva Indifferensi

# Sifat-Sifat Kurva Indifferensi

Dengan memperhatikan bentuk dari sebuah kurva indifferensi, maupun peta indifferensi, maka diketahui bahwa kurva indifferensi ini mempunyai sifat-sifat sebagai berikut: 

1. Sebuah garis yang memiliki arah yang menurun.
2. Cembung terhadap titik nol (0).
3. Tidak berpotongan antara satu kurva indifferensi dengan kurva indifferensi yang lain.
4. Semakin ke kanan dari titik nol (0) posisi sebuah kurva indifferensi, maka kurva indifferensi itu menunjukkan nilai utilitas yang semakin besar. 

Sifat yang menyatakan bahwa slope dari kurva yang menurun dan bentuk kurva indifferensi yang cembung, ini erat kaitannya dengan tingkat substitusi marginal (TSMx-y) dari penggunaan barang X terhadap barang Y. Dan penjelasan TSMx-y diberikan pada bagian berikut.

Gambar 74. Dua Kurva Indifferensi Berpotongan

Kemudian sifat yang menyatakan bahwa kurva indifferensi yang satu tidak pernah berpotongan dengan kurva indifferensi yang lain, ini dapat dijelaskan sebagai berikut. 

• Contoh, ada dua kurva indifferensi yakni Id1 dengan utilitas=20, sedangkan Id2 dengan utilitas=40.
• Jika kedua kurva indifferensi tersebut berpotongan kata kanalah di titik A, maka berarti di titik A ini utilitas masing-masing kurva indifferensi harus sama besar. Tetapi kenyataan menunjukkan yakni; Id1 memiliki nilai utilitas=20, sedangkan Id2 memiliki nilai utilitas=40. Dengan melihat nilai utilitas di titik A yang berbeda dari masing-masing kurva indifferensi tersebut, berarti ini menunjukkan, bahwa kedua kurva tersebut tidak mungkin berpotongan. Kondisi seperti ini dapat dilihat melalui Gambar 72

# Tingkat Substitusi Marginal Barang X-Y 

Tingkat substitusi marginal X-Y (TSMx-y) ini mengukur tingkat penggantian marginal yang timbul akibat dari perubahan penggunaan dari barang X sebesar 1 unit terhadap perubahan penggunaan barang Y.

Notasi : ∆ = perubahan dari masing-masing variabel (yakni X ,Y). 

Di titik A: 

1. Di titik A: Y=6 unit. 

Di titik B: Y=9 unit. 

∆ (By –Ay) = (9 – 6 ) unit=3 unit 

Jadi: ∆ Y = 3.

2. Di titik A:   X=4 unit. 

Di titik B:       X=1 unit. 

∆ (Bx–Ax) = (1 – 4 ) unit=- 3 unit. 

Jadi: ∆ X = -3.

Gambar 75. Dua Kurva Indifferensi Berpotongan

Dengan demikian berarti terjadi perubahan TSMx-y di setiap titik pada setiap titik koordinat yang ada di satu kurva indifferensi. Ini menunjukkan bahwa slope di setiap titik adalah menurun

Bukti dari analisis berikut menunjukkan: 

1) Di titik B dengan slope = -3. 

2) Di titik A dengan slope = -1. 

Bukti ini menandakan bahwa sifat dari kurva indifferensi adalah memiliki slope yang menurun dan juga bentuknya cembung ke arah titik nol (0).

# Hubungan TSMx-y Dengan UM 

Dalam bahasan utilitas marginal (UM) telah diketemukan bahwa, besarnya UM untuk dua jenis barang (yakni X dan Y), sebagai berikut:

Share this post